splay

前言

总所周知，平衡树是一个喜闻乐见的算法，它种类多样，功能强大，应用广泛。

介绍

Splay 树（伸展树），是一种平衡二叉查找树，它通过 Splay/伸展操作 不断将某个节点旋转到根节点，使得整棵树仍然满足二叉查找树的性质，能够在均摊 O(log N) 时间内完成插入，查找和删除操作，并且保持平衡而不至于退化为链。

Splay 树由 Daniel Sleator 和 Robert Tarjan 于 1985 年发明。

Splay 树的 基本思想 是：每次操作都将某节点旋转到根节点，使得整棵树仍然满足二叉查找树的性质。

操作

记号规定

rt：根节点
tot：树的总节点数
fa_i：节点 i 的父节点
ch_i, 0：节点 i 的左孩子
ch_i, 1：节点 i 的右孩子
val_i：节点 i 的值
cnt_i：值 i 出现的次数
sz_i：以节点 i 为根的子树的权值个数（包括重复权值）

基本操作

pushup(x) ：更新节点的 sz

1	void pushup(int x) { sz[x] = sz[son[x][0]] + sz[son[x][1]] + cnt[x]; }

getson(x) ：判断 x 是 fa_x 的左儿子还是右儿子

1	bool getson(int x) { return x == son[fa[x]][1]; }

clear(x) ：销毁节点 x

1	void clear(int x) { son[x][0] = son[x][1] = fa[x] = val[x] = cnt[x] = sz[x] = 0; }

旋转

还记得 Splay 的基本思想吗：

每次操作都将某节点旋转到根节点，使得整棵树仍然满足二叉查找树的性质。

因此旋转操作的本质为将某个节点上升一个位置。

因为 Splay 树是一颗二叉查找树，所以旋转需要保证 Splay 树的中序遍历不变。

在 Splay 中，旋转分为两种：左旋和右旋。

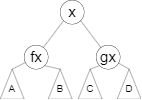
这里我们以右旋为例，详细讲解：

现在有一个节点 x，有他的父节点 fx 和爷爷节点 gx（fa_{fa_x}）。

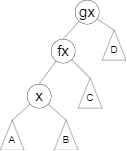
将 x 的 右儿子 设为 fx 的 左儿子，并将它的父亲设为 fx。
son[fx][0]=son[x][1],fa[son[x][1]] = fx;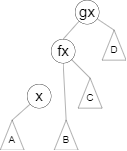
将 fx 设为 x 的 右儿子，并将它的父亲设为 x。
son[x][1]=fx,fa[fx]=x;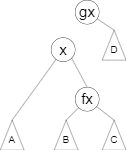
将 x 设为 gx 的 左儿子，并将它的父亲设为 gx。
son[gx][1]=x,fa[x]=gx;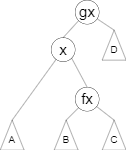

void rotate(int x) {
        int fx = fa[x], gx = fa[fx];
        bool ch = getson(x);
        son[fx][ch] = son[x][ch ^ 1], fa[son[x][ch ^ 1]] = fx;
        son[gx][getson(fx)] = x, fa[x] = gx;
        son[x][ch ^ 1] = fx, fa[fx] = x;
        pushup(fx), pushup(x);
    }

Splay/伸展操作

Splay/伸展操作是 Splay 树的核心操作，它通过旋转操作将某节点旋转到根节点，并将其上升到树的最高层，使得整棵树仍然满足二叉查找树的性质。

同时，Splay 操作规定：每访问一个节点 x 后都要强制将其旋转到根节点。

Splay 操作大体可以分为三种，一共六种情况。

规定记号：

x：待旋转节点
fx：x 的父节点
gx：fx 的父节点

zig：当 fx 为根节点时操作，直接将 x 左旋/右旋到根节点。
zig-zig：当 fx 与 x 都在同一侧子树时操作（即 x、fx、gx 在同一条线上），先将 fx 左旋/右旋，再将 x 右旋/左旋。
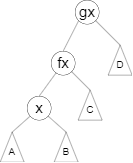
先将 fx 右旋
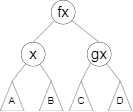
再将 x 左旋
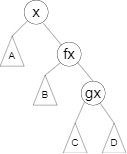
zig-zag：当 fx 与 x 都在不同侧子树时操作（即 x、fx、gx 在不同一条线上），先将 x 右旋/左旋，再将 x 左旋/右旋。
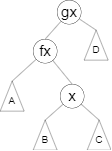
先将 x 左旋
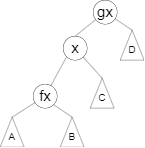
再将 x 右旋